Przeszukiwanie wszerz

Przeszukiwanie wszerz

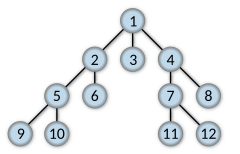Kolejność odwiedzania węzłów
Rodzaj	Przeszukiwanie grafu
Struktura danych	graf, drzewo
Złożoność
Czasowa	$O(|V|+|E|)$
Pamięciowa	$O(|V|+|E|)$

Animowany przykład algorytmu przeszukiwania wszerz

Przeszukiwanie wszerz (ang. breadth-first search, BFS) – jeden z najprostszych algorytmów przeszukiwania grafu. Przechodzenie grafu rozpoczyna się od zadanego wierzchołka s i polega na odwiedzeniu wszystkich osiągalnych z niego wierzchołków. Wynikiem działania algorytmu jest drzewo przeszukiwania wszerz o korzeniu w s, zawierające wszystkie wierzchołki osiągalne z s. Do każdego z tych wierzchołków prowadzi dokładnie jedna ścieżka z s, która jest jednocześnie najkrótszą ścieżką w grafie wejściowym. Algorytm działa prawidłowo zarówno dla grafów skierowanych jak i nieskierowanych.

Algorytm

funkcja BreadthFirstSearch (Graf G, Wierzchołek s)
    dla każdego wierzchołka u z G:
        kolor[u] = biały
        odleglosc[u] = inf
        rodzic[u] = NIL
    kolor[s] = SZARY
    odleglosc[s] = 0
    rodzic[s] = NIL
    Q.push(s)
    dopóki kolejka Q nie jest pusta:
        u = Q.front()
        Q.pop()
        dla każdego v z listy sąsiedztwa u:
            jeżeli v jest biały:
                kolor[v] = SZARY
                odleglosc[v] = odleglosc[u] + 1
                rodzic[v] = u
                Q.push(v)
        kolor[u] = CZARNY

Danymi wejściowymi dla algorytmu jest reprezentacja grafu w postaci listy sąsiedztwa wierzchołków oraz wierzchołek od którego rozpoczynane jest przeszukiwanie. Początkowo wszystkie wierzchołki kolorowane są na biało, co oznacza, że nie zostały jeszcze odwiedzone. Inicjalizowane jest także pole odległości, które zawiera informacje o odległości danego wierzchołka od s oraz pole rodzica, które jest wykorzystywane przy odtwarzaniu drzewa przeszukiwania wszerz. Kolejka FIFO Q jest inicjalizowana węzłem startowym, którego kolor ustawiony został na szaro – oznacza to, że węzeł został już odwiedzony, lecz nie zostały odwiedzone węzły do niego sąsiednie. Następnie, pobierany jest pierwszy wierzchołek z kolejki i analizowana jest lista jego sąsiadów. Jeżeli sąsiad jest biały, oznacza to, że nie został jeszcze odwiedzony: aktualizowane są więc pola odległości i rodzica oraz jego kolor a następnie jest on dodawany do kolejki. Po przejrzeniu wszystkich sąsiadów danego węzła kolor węzła bieżącego zmieniany jest na czarny (wszyscy jego sąsiedzi zostali odwiedzeni) i operacja powtarza się dla następnego węzła znajdującego się w kolejce, bądź też (jeżeli kolejka jest pusta) algorytm kończy swoje działanie.

Właściwości

Złożoność pamięciowa

Złożoność pamięciowa algorytmu uzależniona jest od tego w jaki sposób reprezentowany jest graf wejściowy. W przypadku listy sąsiedztwa dla każdego wierzchołka przechowywana jest lista wierzchołków osiągalnych bezpośrednio z niego. W tym wypadku złożoność pamięciowa wynosi O(|V| + |E|) (zob. Asymptotyczne tempo wzrostu), gdzie |V| to liczba węzłów, a |E| to liczba krawędzi w grafie, odpowiadająca sumie wierzchołków znajdujących się na listach sąsiedztwa.

W przypadku macierzy sąsiedztwa wymagane jest przechowywanie macierzy o wymiarach |V|x|V|, czyli potrzebne jest O(|V|²) pamięci.

Złożoność czasowa

Ponieważ w najgorszym przypadku przeszukiwanie wszerz musi przebyć wszystkie krawędzie prowadzące do wszystkich węzłów, złożoność czasowa przeszukiwania wszerz wynosi O(|V| + |E|), gdzie |V| to liczba węzłów, a |E| to liczba krawędzi w grafie.

Kompletność

Przeszukiwanie wszerz jest kompletne, to znaczy, że gdy istnieje rozwiązanie, przeszukiwanie wszerz odnajdzie je niezależnie od grafu.

Zastosowania

Przeszukiwanie wszerz może zostać użyte do rozwiązania wielu problemów z teorii grafów, dla przykładu:

• Odnalezienie wszystkich połączonych węzłów w grafie
• Odnalezienie najkrótszej ścieżki między dwoma wierzchołkami (nie uwzględnia wag krawędzi w grafie ważonym)
• sprawdzania czy graf jest dwudzielny

Zobacz też

• Przeszukiwanie w głąb